QUBO++とは?
QUBO++は、さまざまな最適化問題を HUBO (High-order Unconstrained Binary Optimization) に記号処理で変換し、QUBO/HUBO を効率良く構築・探索するためのC++ベースのライブラリとソルバー群です。
与えられた組み合わせ最適化問題をQUBO/HUBO問題に変換し、解を探索するまでの一連のプロセスをシームレスに開発できます。
マルチスレッド対応の高速な変換機能、QUBOソルバー、外部ソルバーとの連携を可能にするAPIを備えています。
QUBO++が注目される理由
組み合わせ最適化問題は、
- 物流の効率化
- エネルギー消費の最小化
- スケジューリングの最適化
など、現代社会の幅広い分野で重要な役割を果たしています。
これらの課題を効率的に解くことは、社会的コストの削減や持続可能な社会の実現に直結するため、極めて重要です。
しかし、各課題に特化した専用ソルバーを開発するには、高度な専門知識と膨大なコストが必要であり、実装のハードルが高いのが現状です。
QUBO問題というアプローチ
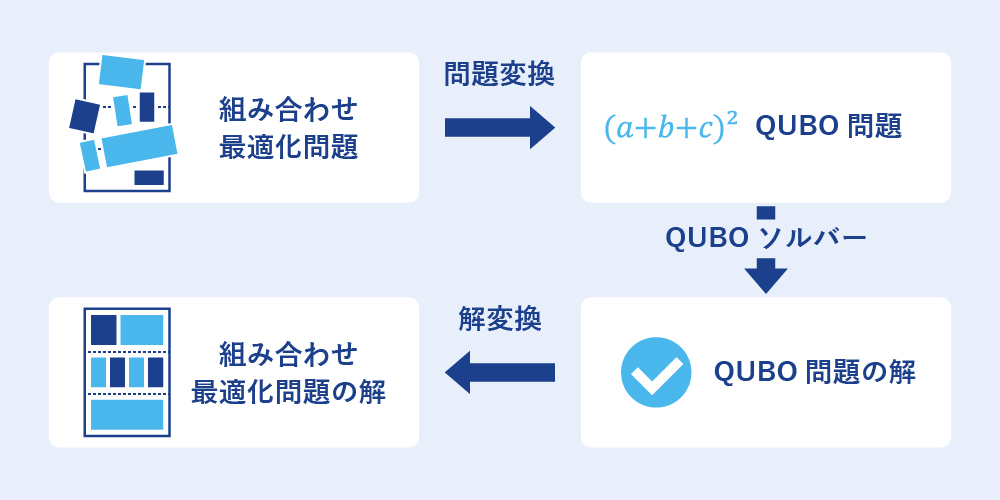
多くの組み合わせ最適化問題は、QUBO(Quadratic Unconstrained Binary Optimization)問題に変換できることが知られています。
この性質を活用することで、より効率的な解法を構築することが可能になります。
具体的には、以下の3ステップで最適化計算を行います。
- 解きたい組み合わせ最適化問題をQUBO形式に変換する
- QUBOソルバーを用いて最適解を探索する
- 得られた結果を元の問題の解に逆変換する
このアプローチにより、高性能なQUBOソルバーを利用すれば、変換処理と逆変換処理の開発だけで、複雑な組み合わせ最適化問題に対して高精度な解を得ることができます。
QUBO++を用いた最適化計算の流れ
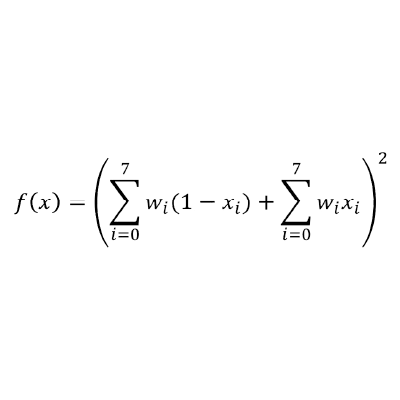
課題を組み合わせ最適化問題として定式化します。

QUBO++クラスを利用したコーディングを行います。
- QUBO/HUBO、イジングモデル
- QUBO式の自動生成

高性能なソルバーで、一般的なPCでも高速な計算が期待できます。
- Easy Solver(ヒューリスティック型)
- Exhaustive Solver(全探索型)
- ABS3(GPUソルバー)
-
Feature 01
簡潔なC++17ベースの設計
基本的な3つのC++クラス、変数(qbpp::Var)、式(qbpp::Expr)、解(qbpp::Sol)を理解すれば、QUBO/HUBO問題を扱うC++コードを簡単に作成できます。
QUBO++ ライブラリは、変数を含む多項式を設計するための次のコア クラスを提供します。
クラス 役割 qbpp::Var 単一のシンボリック変数を格納 qbpp::Expr qbpp::Var オブジェクトの多項式を格納 qbpp::Sol qbpp::Expr オブジェクトのソリューションを格納 qbpp::VarInt 整数を表す qbpp::Var オブジェクトのセットを格納 qbpp::Term qbpp::Expr オブジェクトに含まれる単一の用語を格納 -
Feature 02
HUBO対応
2次に限定されるQUBOだけでなく高次のHUBOも扱えます。
16次項までのHUBO式にネイティブに対応
・通常のQUBOソルバーはHUBOを次数削減によりQUBO化して解く
・次数削減の問題点:補助変数の増加・項数の爆発
・大量の非最適局所最適解にトラップされ,真の最適解を得るのが困難になる
QUBO++のHUBOソルバーは、次数削減せず、直接探索で元の式の構造を保持して計算します -
Feature 03
QUBO/HUBO 組み込みソルバー
CPUソルバー: Easy Solver(ヒューリスティック型)およびExhaustive Solver(全探索型)
GPUソルバー:ABS3
3つのソルバーを同梱しています。■ Easy Solver(ヒューリスティック型)
ヒューリスティックアルゴリズムにより解探索。単純ながら比較的高い解探索能力を備えています。
・マルチコアCPUの並列スレッドを活用した高速並列探索
・シミュレーティッドアニーリングなどの複数の局所探索アルゴリズムを同時実行■ Exhaustive Solver(全探索型)
全解探索。小規模QUBO問題で、すべての最適解を列挙できるため、デバッグに活用できます。
・マルチコアCPUの並列スレッドを活用した高速並列探索
・デバッグ用途:全解を探索し,厳密解を必ず求める
・実利用可能な二値変数の個数の上限:30〜40程度■ ABS3 GPU Solver
マルチGPUでヒューリスティックアルゴリズムにより解探索を行うQUBO/HUBOソルバーです。
・GPUのCUDAコアをフルに活用し並列解探索を行う
・複数のGPUを用いた並列処理に対応
・遺伝的アルゴリズム+シミュレーティッドアニーリングによる局所探索をCUDAコアで並列実行Gurobi Optimizer(API)を QUBO++ から直接呼び出すことも可能です。
-
Feature 04
並列処理による高速化
Intel® Threading Building Blocks(TBB)によるマルチスレッド化で、高速な記号処理と変換を実現します。
-
Feature 05
高い移植性
BoostやTBBなどの標準的なライブラリのみを利用し、Linuxベースの多くの計算機で動作します。
さらに、WindowsのWSLやmacOS(Intel/ARM)でも動作確認済みです。 -
Feature 06
変数制限、演算子、関数
桁数制限のない整数:多倍長整数をサポートし、式の定数項や係数として桁数制限のない値を使用できます。
整数変数のサポート:整数変数を扱えるため、整数計画問題をQUBO形式で簡単に記述できます。
多彩な演算子と関数:ベクトル演算を含む複雑な式を操作するための豊富な演算子と関数が用意されています。
Isingモデルの生成:スピン変数(−1/+1−1/+1)を使用したIsingモデルの生成が可能です。
QUBO++プログラムの例
次のような3変数を含む関数があるとします。
このときの最適解は(エネルギー最小値が0となる) \[ (a,b,c)=(0,0,0),(1,1,0),(0,0,1) \] で、これらはいずれも \( f(a,b,c)=0 \) を与えます。
QUBO++ を用いたプログラムは、以下のように記述できます。
<QUBO++プログラム>
#include "qbpp.hpp"
#include "qbpp_exhaustive_solver.hpp"
int main() {
auto a = qbpp::var("a"); // 変数の作成
auto b = qbpp::var("b");
auto c = qbpp::var("c");
auto f = (a + b + c) * qbpp::sqr(a + 2 * b + 3 * c - 3); // 多項式の記述
std::cout << "f = " << f.simplify_as_binary() << std::endl; // 多項式の整理
auto solver = qbpp::exhaustive_solver::ExhaustiveSolver(f); // QUBO式の最適解の求解
auto sols = solver.search_optimal_solutions(); // 全ての最適解の探索
std::cout << sols << std::endl; // 得られた解の表示
}
また以下のような式(重み係数やペナルティ関数の考慮)も簡単に入力することができます。
auto x = qbpp::var("x", graph_map.node_count(), color_count);
auto f = qbpp::sum(qbpp::sqr(qbpp::sum(x) - 1));
for (auto [i, j] : graph_map.get_edges())
f += qbpp::sum(x[i] * x[j]);